150 . 關鍵邏輯閘
TopCoder
Description
一個組合電路(combinational circuit)由線路(wires)連接一組邏輯閘(logic gates)而成,並且不包含有向迴路(directed cycle)。一個組合電路的效能決定於最後一個主要輸出(primary output)被算出來的時間。假設每一個邏輯閘所需的運算時間都是固定並且是已知的,而線路的延遲(delay)是0。我們希望把一個組合電路所有的關鍵邏輯閘找出來。若一個邏輯閘的運算時間有任何延長,便會影響到整個電路的效能,它就被稱為關鍵邏輯閘。
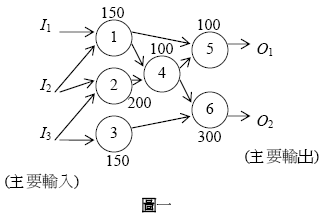
以圖一的組合電路為例,I1、I2、I3是主要輸入;O1、O2是主要輸出;圓圈代表邏輯閘,箭頭代表線路;每個邏輯閘有自己的編號以及固定的延遲時間。在圖一的例子當中,該組合電路中的O1會因為邏輯閘2、4、5的延遲,在時間400才會收到運算結果;而O2會因為邏輯閘2、4、6的延遲,在時間600才收到運算結果,因此O2是最後一個被算出來的主要輸出。關鍵邏輯閘分別是2、4以及6號邏輯閘,當其中一個關鍵邏輯閘的運算時間有任何延長,O2被算出來的時間也會再往後延遲。相反地,就算1號邏輯閘的運算時間從150延長到160,也不會影響到O2被算出來的時間,因此1號邏輯閘並不是關鍵邏輯閘。
Input Format
第一行為一個整數 $n$,代表一個組合電路的邏輯閘總數,每個邏輯閘的編號都不同,且範圍是介於 $1$~$n$ 之間的整數。第二行為一個整數 $m$,代表線路的總數。接下來的 $n$ 行,依序列出每個邏輯閘的運算時間;每個運算時間的值是介於 $0$ 到 $600$ 之間(含)的整數。最後 $m$ 行,分別列出每一條線路由某個邏輯閘的輸出接到另一個邏輯閘的輸入。
注意:為簡化輸入,我們把主要輸入(primary inputs)與邏輯閘之間的線路,以及邏輯閘與主要輸出(primary outputs)之間的線路省略。(每一個邏輯閘至少都含有一個線路輸出到另一個邏輯閘或主要輸出)
$1 \leq n \leq 100000$,$0 \leq m \leq 300000$
Output Format
列出關鍵邏輯閘的個數。
Sample Input 1
6
150
200
150
100
100
300
1 5
1 4
2 4
4 5
4 6
3 6
Sample Output 1
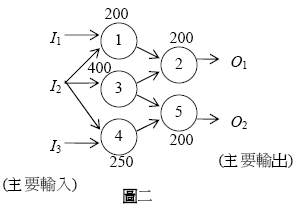
Sample Input 2
4
200
200
400
250
200
1 2
3 2
3 5
4 5
Sample Output 2
Hints
Problem Source
NEOJ Problem 164
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~9 | 100 |
